새로운 방법론의 필요성
지금까지 배운 강화학습 지식을 이용해 어떤 문제에 대해 강화학습 알고리즘을 적용하고 싶다면 다음과 같은 결정트리(Decision Tree)를 이용할 수 있다.
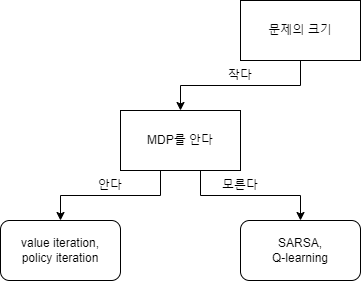
우리는 지금까지 MDP의 크기가 작을 때 적용할 수 있는 테이블 기반 방법론에 대해 배웠다. MDP의 크기가 클 때 테이블 기반 방법론을 사용하지 못하는 이유는 간단하다. 테이블을 만들 수 없기 때문이다. 예를 들어 바둑의 고유한 상태의 개수는 $10^{170}$개이고 $10^{170}$B를 저장할 수 있는 컴퓨터는 아직 이 세상에 없다. 만약 $10^{170}$개의 상태를 저장할 수 있다고 해도 제대로 된 학습이 이루어지기 위해서는 각상태를 여러 번 방문해봐야 한다. 따라서 MDP의 크기가 큰 경우에는 새로운 방법론이 필요하다. 이번 포스팅에서는 MDP의 크기가 클 때 사용될 수 있는 방법론을 배워본다.
밸류 네트워크(Value Network)
만약 입력값으로 상태, 행동 정보를 주었을 때 실제가치의 근사치를 출력하는 함수가 있다면 어떨까? 우리는 더 이상 테이블에 모든 추정값을 저장할 필요가 없어진다. 단지 함수를 구성하는 파라미터$\theta$만 저장하면 된다.
$$Q(s, a; \theta) \approx q_\pi(s, a)$$
이러한 방식은 경험하지 않은 상태에 대해서도 가치를 예측할 수 있게 해 준다.(물론 가운데처럼 잘 학습되었을 때 이야기다)
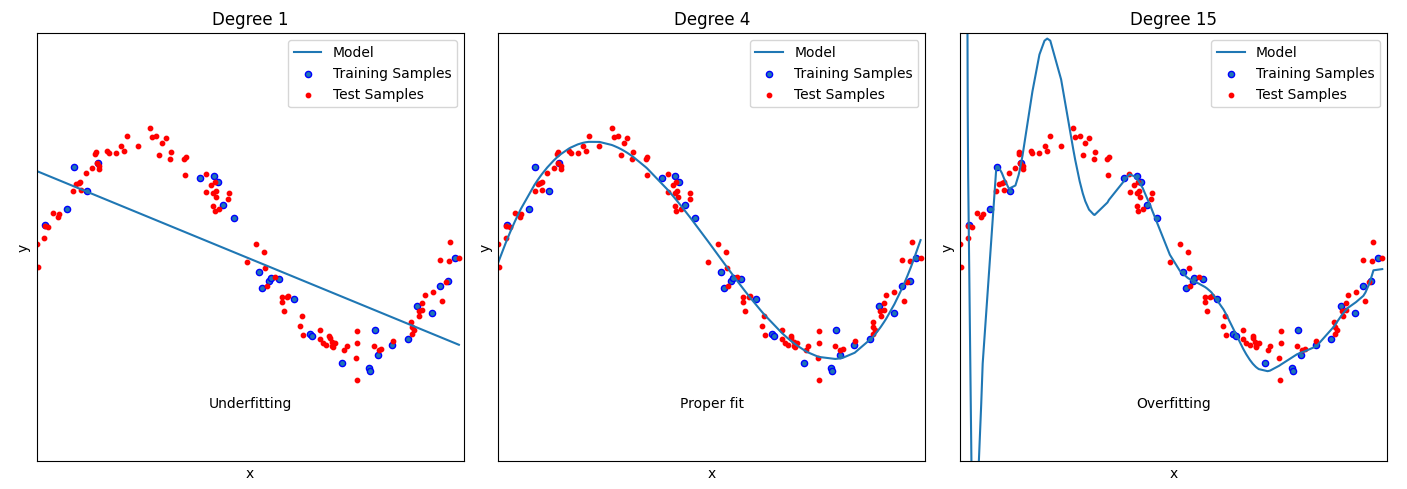
그렇다면 근사함수로 어떤 함수를 이용해야 할까? 현대 강화학습에서 그 답은 DNN(Deep Neural Networks)이다. 강화학습의 역사는 신경망의 사용이전과 이후로 나뉜다. 이는 신경망이 강화학습에 혁신적인 변화를 가져왔음을 의미한다. 신경망 기반의 근사함수를 밸류 네트워크라고 부른다.
밸류 네트워크의 학습
학습이 완료된 밸류 네트워크의 경우 상당한 이점이 있다는 걸 확인했다. 그렇다면 어떻게 밸류 네트워크를 학습시킬 수 있을까? 그전에 기존의 가치함수 업데이트의 형태를 살펴보자.
$$Q(s, a) \leftarrow Q(s, a) + \alpha(Q_{true}(s, a) - Q(s, a))$$
기존의 가치함수의 업데이트가 예측값이 정답에 조금 더 가까워지도록 예측값 자체를 업데이트하는 형태라면, 밸류 네트워크의 경우 예측값이 정답에 조금 더 가까워지도록 파라미터를 업데이트한다. 이 과정은 3단계로 이루어진다
- 손실함수를 정의
$L(\theta)$ - 그레디언트 계산
$\nabla_\theta L(\theta)$ - 파라미터 업데이트
$\theta \leftarrow \theta - \alpha \nabla_\theta L(\theta)$
(필요에 따라 2~3 과정은 n번 반복된다)
DQN
2015년에 구글의 DeepMind팀에 의해 개발된 DQN은 " Human-level control through deep reinforcement learning "이라는 논문을 통해 세계에 처음 소개되었으며, Atari 2600 게임을 인간과 유사한 수준으로 플레이하며 강화학습 분야에 큰 반향을 일으켰다. DQN은 단순히 기존 Q-learning 알고리즘에 신경망을 결합한 것이 아닌, 두 가지 방법론(experience replay, target network)을 추가적으로 적용하여 성능을 대폭 향상했다.
- experience replay
에이전트가 환경과 상호작용하면서 얻은 경험은 Replay Buffer에 저장된다. 이 저장소는 제한된 크기를 가지며, 새로운 경험이 추가될 때 가장 오래된 경험이 제거된다. 학습과정에서 에이전트는 Replay Buffer에서 무작위로 일정수의 경험을 샘플링해 배치를 구성한 후 학습한다. 이 과정을 통해 같은 경험을 여러 번 활용할 수 있게 되어, 한정된 경험으로부터 많은 학습을 이끌어낼 수 있다. - target network
파라미터가 업데이트될 때 예측값뿐만 아니라 정답 역시 영향을 받는다. 이는 원치 않았던 결과로, 정답지가 계속해서 변하는 것은 학습의 안정성을 떨어뜨린다. target network는 이러한 문제를 해결하기 위한 직접적인 방법으로, 고정된 파라미터를 가지고 있어 학습 시 일정한 정답을 제공한다. 더불어, 주기적으로 main network로부터 파라미터를 가져와 지금까지의 학습 진행 상황을 반영하도록 업데이트된다.
이러한 개선은 DQN의 손실함수에 반영되어 있으며, 손실함수는 다음과 같이 정의 내릴 수 있다.
$$L(\theta) = \mathbb {E} \left [ \left( r + \gamma \max_{a'} Q(s', a'; \theta^-) - Q(s, a; \theta) \right)^2 \right]$$
- $\mathbb {E}[\cdots]$: 배치안의 다양한 경험들로부터 계산된 손실값들의 평균
- $(\cdots)^2$: MSE(평균제곱오차)
- $\theta^-$: target network의 고정된 파라미터
'공부 정리 > 강화 학습' 카테고리의 다른 글
| [강화학습9]Q-learning (0) | 2023.12.05 |
|---|---|
| [강화학습8]SARSA (0) | 2023.12.03 |
| [강화학습7] MC(Monte Carlo Methods)와 TD(Temporal Difference Learning) (0) | 2023.12.01 |
| [강화학습6]정책 반복(Policy Iteration) (0) | 2023.10.25 |
| [강화학습5]최적 정책(Optimal Policy) (0) | 2023.10.09 |




댓글